Details of Beam Diameter
The beam diameter or beam width of an electromagnetic beam is the diameter along any specific line that is perpendicular and intersects the beam axis. The diameter can be defined in various ways due to the beam’s blunt edges. There are five definitions of the beam width: D4 σ, 10/90 or 20/80 knife-edge, 1/e2, FWHM, and D 86. The beam width is measured not only in units of length at a particular plane perpendicular to the beam axis but in reference to the angle, angular width from the light source. This angular width is also called the beam divergence.
Beam diameter is typically used for characterization of the electromagnetic beam in the optical region, and occasionally in the microwave region, that is, cases in which the aperture from which the electromagnetic beam is very large with respect to the wavelength.
Beam diameter usually refers to the circular cross-section. In some beams that have an elliptical cross-section, their beam diameters must be specified as the length of either the major or minor axis of the elliptical section. The term “beam width” is preferred in applications where the beam does not have circular symmetry.
1. Definitions
1.1. Rayleigh Beam Width
Rayleigh beamwidth is the angle between the maximum peak and the first null of radiated power.
1.2. FWHM (full width at half maximum)
The most convenient way to define the width is to choose two diametrically opposite points at which the irradiance is a specified fraction of the beam’s peak irradiance, and take the distance between them as a measure of the beam’s width. The fraction is typically 1/2 (-3 dB), and refers the full width of the beam at half its maximum intensity to the beam diameter (FWHM). This is also known as half-power beam width (HPBW).
1.3. 1/e2 width
The 1/e2 width is equal to the distance between the two points corresponding to the maximum value, 1/e2 = 0.135 times. It is often logical to take a distance between two points that are the maximum intensity, 1/e2 = 0.135 times. In the case of more than two points that are 1/e2 times the maximum value, the two points closest to the maximum value are choosen. The 1/e2 beam width is mathematically important in Gaussian beams. The intensity profile of a Gaussian beam is expressed by the following equation.
![]()
The American National Standard Z136.1-2007 for Safe Use of Lasers (p. 6) defines the beam diameter as the distance between the diametrically opposing points in the cross section of the intensity distribution of a beam where the power per unit is 1/e (0.368) times that of the peak power of per unit area. This is available for computing the maximum allowable exposure (MPE). The Federal Aviation Administration uses the 1/e definition to calculate laser safety in FAA Order 7400.2 F, Procedures for Handling Airspace Matters (February 16, 2006, p. 29 -1 -2.).
Unlike D4σ and knife-edge width depending on the integral of the intensity distribution, the measurement of the 1/e2 width depends on three points of the intensity distribution. Measurement of the 1/e2 width greates more noises than that of the D4σ width. For multimodal intensity profiles (beam profiles with multiple peaks), the 1/e2 width measurement fails to obtain a meaningful value, which results in grossly small estimates of inherent beam width. The D4σ width is appropriate for multimodal intensity distributions. An ideal single-mode Gaussian beam gives the same measured values of D4 σ, D 86 and 1/e2 widths.
Gaussian beam expresses the following equation in the relationship between the 1/e2 width and the full width at half maximum.
![]()
2w is the full width of the beam at 1/e2.
1.4. D4σ or second-moment width
The D4σ width of a beam in the horizontal or vertical direction is four times σ, where σ is the standard deviation of the horizontal or vertical intensity distribution respectively.
The D4σ beam width in the x direction for the beam profile is expressed by the following equation.
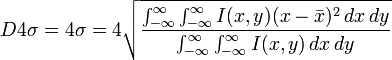
This equation is the average of the beam profile in the x direction.
![]()
In measurement of the beam with a laser beam profiler, the wings of the beam profile influence the D4σ value more than the center of the profile because the wings squared or x2 of its distance from the center of the beam. The beam which is less than 1/3 of the beam profiler’s sensor area, has a significant number of pixels with low baseline values (background values) at the edge of the sensor. In the larger baseline values or not subtracted from the image, the calculated D4σ value is larger than the actual value, for the integral value of D4σ at two times includes the baseline value near the edge of the sensor. Therefore, subtraction of the baseline value is essential for accurate D4σ measurement. Recording the average value of each pixel in non-irradiated laser lights can measure the baseline values. Unlike the FWHM and the 1/e2 width, the D4σ width is effective for a multimodal intensity distribution which is a beam profile with multiple peaks. However, accurate subtraction of the baseline value requires an accurate result. D4σ is the ISO international standard for beam width.
1.5. Knife-edge width
Prior to the CCD beam profiler, the knife-edge method in which slicing the laser beam with a razor to measure the power of the sliced beam as a function of the position of the razor was applied to estimate the beam width. The measured curve is an integral of the intensity distribution, starting with the total intensity of the beam and decreasing monotonically by the null integral. The beam width defines the distance between two points of the measured curve that are 10% and 90% (or 20% and 80%) of the maximum value. In small or subtracted baseline values, the knife-edge beam width of any beam profile corresponds to 60% of the total beam power at 20/80 and 80% of the total beam power at 10/90. On the other hand, D4σ, 1/e2, and FWHM widths are affected by the intensity distribution depending on the beam shape. Therefore, the 10/90 or 20/80 knife-edge width is suitable to ensure that the width contains a percentage of the total beam power. Most CCD beam profiler’s software can compute the knife-edge width numerically.
1.6. Fusing knife-edge technology with imaging
The main drawback of the knife-edge method is plotted measurements only on the scanning direction, which minimizes the amount of relevant beam information. To overcome this drawback, an innovative technique like an intensity distribution of a beam that scans a knife-edge in multiple directions to produce a knife-edge image, is also commercially offered. (http://www.novuslight.com/laser-beam-profiling-and-measurement_N678.html)
This technique ensures that the amount of energy impinging the sensor area can be determined by the obstruction by moving the knife edge mechanically across the beam. The beam profile is measured from the relations between the knife-edge velocity and the energy value from the detector. Unlike other systems, a unique scanning technique that sweeps knife-edge s in different directions across the beam is used.
With tomographic reconstruction, mathematical processes reconstruct beam sizes in various directions as an image that is similar to the one produced by CCD cameras. The main advantage of this scanning method is that it is free from pixel size limitations like CCD cameras and allows beam reconstruction with wavelengths that are unavailable with existing CCD technology. Reconstruction of deep UV to far IR beams is possible.
1.7.D 86 width
The D 86 width is defined as the diameter of a circle that is centered at the centroid of the beam profile and contains 86% of the beam power. The solution for D 86 width is found by computing the area of increasingly larger circles around the centroid of the beam profile until the area contains 86% of the beam power. Unlike previous beam width definitions, the D 86 width is not derived from the intensity distribution. The percentage of 86, rather than 50%, 80%, 90% is chosen because a circular Gaussian beam profile integrated down to 1/e2 of its peak value contains 86% of the total power. The D 86 width is often used in applications that need exact knowledge of how much power is in a given area. Applications of High-energy laser weapons and LiDAR (lidars) require precise information about how much power illuminates the target.
1.7.1 Beam width for elliptical beams
The previous definitions hold for stigmatic (circular symmetric) beams only, while astigmatic beams require a more rigorous definition of the beam width. The definition of the beam width is expressed by the following equation.
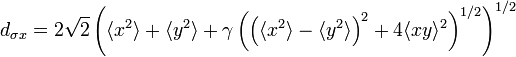
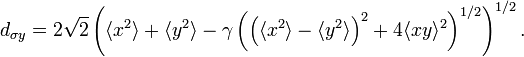
This includes the X-Y correlation beam diameter, but both two equations for circular symmetric beams are the same. Some new symbols within the equations are the first and second moments of the area.
![]()
![]()
![]()
![]()
![]()
The beam power P is the following equation.
![]()
![]()
Using this general definition, the beam azimuthal angle ![]() can also be expressed as follows.
can also be expressed as follows.
![]()
2. Measurement
International standard ISO 11146 ‐ 1: 2005 specifies methods for measuring beam widths (or diameters), divergence angles, and beam propagation ratios of stigmatic laser beams. For general astigmatic beams, ISO 11146 ‐ 2 is applicable. The D4σ beam width is the ISO standard definition, and the measurement of the M2 beam quality parameter requires the D4σ widths. The other definitions provide complementary information for D4σ. D4σ and knife-edge widths are sensitive to the baseline value, whereas 1/e2 and FWHM widths are not. The fraction of total beam power encompassed within the beam width depends on the definition for use. The laser beam widths can be measured by capturing an image on a camera or by using a laser beam profiler.